克鲁斯卡尔算法，什么是克鲁斯卡尔算法

克鲁斯卡尔算法是求连通网克鲁斯卡尔算法的最小生成树的另一种方法以下是关于克鲁斯卡尔算法的详细介绍算法特点时间复杂度克鲁斯卡尔算法的时间复杂度为O克鲁斯卡尔算法，其中e为网中的边数这使得该算法在边稀疏的网中表现尤为出色适用场景由于时间复杂度的特性，克鲁斯卡尔算法更适合用于求解边数相对较少而顶点数较多的克鲁斯卡尔算法；选取第二小的边 AC，选取第三小的边 AB，选取第四小的边 BD，克鲁斯卡尔算法我们得到了这个无向图的最小生成树如上图所示代码方面，例如getAllEdgessortEdgesfindunion等方法就不一一赘述了，你可以点击连接查看完整的Kruskal代码测试效果方面，普利姆Prime算法和克鲁斯卡尔Kruskal。

克鲁斯卡尔算法是求连通网的最小生成树的另一种方法，尤其适合于边稀疏的网以下是关于克鲁斯卡尔算法的详细介绍一算法特点 时间复杂度克鲁斯卡尔算法的时间复杂度为O，其中e为网中的边数这一特点使得该算法在处理边数相对较少而顶点数较多的网络时具有优势二基本思想 初始状态假设连通网；克鲁斯卡尔算法是一种用来寻找加权无向图的最小生成树的算法其要点如下算法核心在所有未选取的边中，选择一条权值最小的边如果这条边与已选取的边不构成回路，则将其加入生成树中如果构成回路，则放弃这条边，选择下一条权值较小的边进行尝试基本思想初始时，构造一个只包含所有顶点边集为空的子图，将。

克鲁斯卡尔算法和普里姆算法得出的结果是一样的嘛

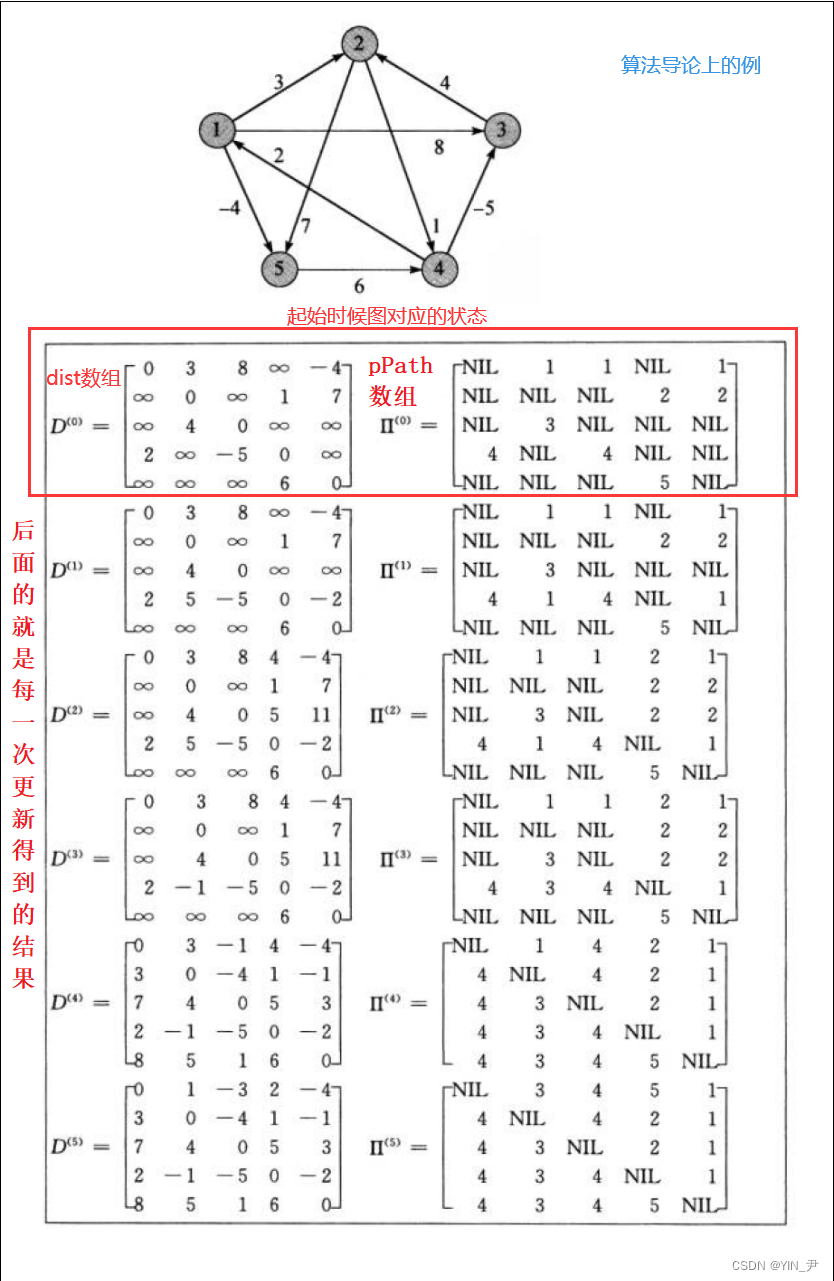
克鲁斯卡尔算法的基本思想1 目标克鲁斯卡尔算法Kruskal#39s Algorithm旨在求解加权连通图的最小生成树Minimum Spanning Tree， MST最小生成树是指连接图中所有顶点的边的集合，且边的总权重最小2 贪心策略该算法采用贪心策略，每一步都选择当前可用的权重最小的边，但有一个关键条件。

克鲁斯卡尔算法是求连通网的最小生成树的另一种方法，尤其适合于边稀疏的网以下是关于克鲁斯卡尔算法的详细介绍算法特点时间复杂度克鲁斯卡尔算法的时间复杂度为O，其中e为网中的边数适用场景由于该算法的时间复杂度与边的数量成对数关系，因此它特别适合于求解边相对较少的稀疏网络的最小生成。

克鲁斯卡尔算法步骤

克鲁斯卡尔算法是一种用来寻找最小生成树的算法以下是关于克鲁斯卡尔算法的详细解答1 算法基本思想 先构造一个只含n个顶点边集为空的子图 将子图中各个顶点看成各棵树上的根结点 从网的边集E中选取一条权值最小的边 若该条边的两个顶点分属不同的树，则将其加入子图，即将两棵。

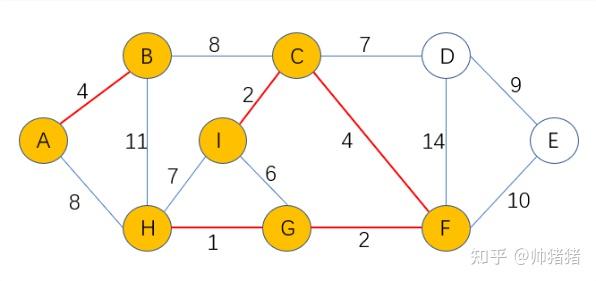
克鲁斯卡尔算法是一种寻找最小生成树的算法该算法的核心在于，从剩余的所有未选取的边中，选择最小边如果这条边与已选取的边构成回路，则放弃这条边，转而选取次小边该算法的基本思想是从一个只包含n个顶点边集为空的子图开始在这个子图中，每个顶点被视为独立的一棵树上的根结点接着。

克鲁斯卡尔算法Kruskal#39s Algorithm是一种用于解决最小生成树问题的贪心算法最小生成树问题是在一个连通加权无向图中寻找一棵包含所有顶点的树，同时这棵树的边权值之和最小克鲁斯卡尔算法的基本思想是按照边的权值从小到大的顺序选择边，并确保选择的边不构成环算法的实现过程中，我们使用一个。

克鲁斯卡尔算法是一种用于求连通网最小生成树的另一种方法与普里姆算法相比，克鲁斯卡尔算法的时间复杂度为Oeloge，其中e为网中的边数因此，它更适合于求边稀疏的网的最小生成树克鲁斯卡尔算法从另一个角度求网的最小生成树其基本思路如下假设有一个连通网G=V，E，其中V代表顶点。

上一篇： 高分影视盒子播放器，高分影视盒播放器下载 app

下一篇： 哈工大深圳考研炸了，哈工大深圳研究生难考吗