完全二叉树，完全二叉树不存在度为1的结点

完全二叉树与满二叉树完全二叉树的区别为性质不同包含不同叶子结点不同一性质不同 1完全二叉树深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时，称为完全二叉树2满二叉树如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

满二叉树和完全二叉树在定义节点分布特征及节点总数规律上存在明显区别，具体如下定义差异满二叉树每个层的节点数均达到最大值若二叉树层数为$K$，则节点总数为$2^K 1$例如，深度为$3$的满二叉树，节点总数为$2^3 1 = 7$完全二叉树深度为$K$的二叉树，若其节点与同深度。

完全二叉树和满二叉树的区别1 定义上的不同 满二叉树除最后一层外，每一层都被完全填充，并且所有叶子节点都集中在该树的最后一层也就是说，每个节点要么是叶节点，要么就有两个子节点完全二叉树除完全二叉树了最底层外，其他层的节点数达到最大，且最底层尽可能集中地保持左倾状态也就是说。

定义上的区别完全二叉树深度为k，有n个结点的二叉树，当且仅当其每一个结点，都与深度为k的满二叉树中编号从1至n的结点逐一对应这意味着，在完全二叉树中，除了最后一层外，每一层上的结点数都达到最大，且最后一层的结点都靠左对齐满二叉树深度为k，且有2的k次方减1个节点的二叉树。

而完全二叉树，在最后一层的节点是可以缺少的，其节点数可能是倒数第二层节点数的2倍满二叉树一定是完全二叉树，也可能是1个，2个，只不过，这些缺的节点只能是最右边的完全二叉树的定义深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一。

1完全二叉树若设二叉树的高度为h，除第 h 层外，其它各层 1～h1 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树2满二叉树除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树3平衡二叉树平衡二叉树又被。

完全二叉树定义完全二叉树是一种特殊的二叉树，除了最后一层外，每一层的节点都被填满，且最后一层的节点从左到右依次填充，不留空缺特点具有良好的平衡性，高度通常较小相对于节点数量可以用数组高效存储和转换满二叉树定义满二叉树是一种更加特殊的完全二叉树，所有层的节点都被。

答案A 第6层有叶结点则说明完全二叉树的高度可能为6或7，显然树高为6时结点最少若第6层上有8个叶结点，则前5层为满二叉树，故完全二叉树的结点个数最少为251+8=39个结点。

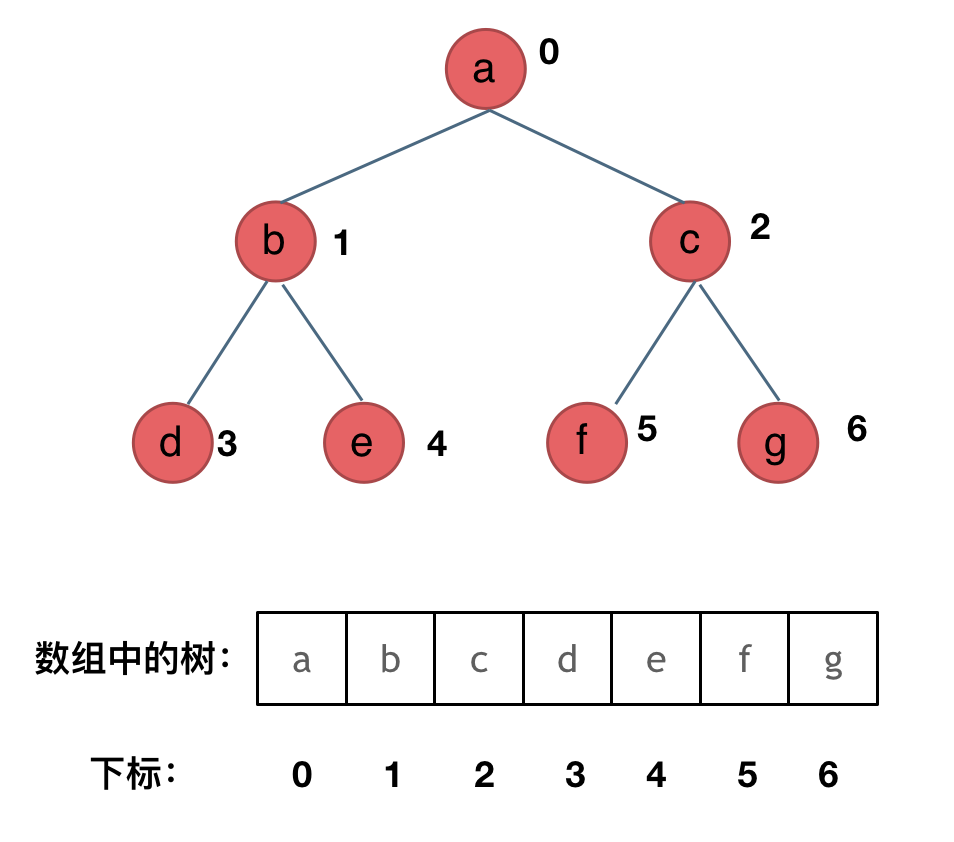
完全二叉树是由满二叉树而引出来的对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树2表示不同对于满二叉树，除最后一层无任何子节点外，每一层上的所有结点都有两个子结点二叉树而完全二叉树是效率很高的。

一棵深度为k，且有2^k1个结点的二叉树，称为满二叉树这种树的特点是每一层上的结点数都是最大结点数而在一棵二叉树中，除最后一层外，若其余层都是满的，并且或者最后一层是满的，或者是在右边缺少连续若干结点，则此二叉树为完全二叉树具有n个结点的完全二叉树的深度为floorlog2n+1深度为k的完全二叉树，至少有2k1个叶子结点，至多有2k1个。

完全二叉树和满二叉树的主要区别如下节点数量完全二叉树节点数量不固定，但满足每个节点都与深度相同的满二叉树中编号从1至n的节点逐一对应满二叉树节点数量固定，为2的k次方减1节点分布完全二叉树叶子节点只可能在层次最大的两层上出现，且对任一节点，若其右分支下子孙的最大层次为。

满二叉树和完全二叉树的主要区别如下节点结构满二叉树每个节点都有左右子节点这种结构使得满二叉树具有高度的规律性完全二叉树节点不必全部填满，允许部分节点为叶节点或没有左右子节点但在最底层，节点会尽可能地从左到右填充紧凑性与灵活性满二叉树结构紧凑且规律，所有层级的节点都。

满二叉树在存储数据时非常高效，因为它充分利用了每个节点的空间，没有浪费然而，在实际应用中，由于数据量的不确定性和动态变化，很难保证树始终保持满二叉树的状态2完全二叉树 完全二叉树是由满二叉树转化而来的它的定义是一棵二叉树，除最后一层外，每一层都是满的，且最后一层的节点都。

1含义不同完全二叉树是由满二叉树而引出来的对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树2表示不同对于满二叉树，除最后一层无任何子节点外，每一层上的所有结点都有两个子结点二叉树而完全二叉。

满二叉树和完全二叉树的区别1完全二叉树是由满二叉树而引出来的对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

满二叉树与完全二叉树的区别主要体现在性质包含关系以及叶子节点的分布上一性质不同 1 完全二叉树一棵深度为k，拥有n个节点的二叉树，如果它的每个节点都能够与深度为k的满二叉树中的编号1到n的节点一一对应，那么这棵树被称为完全二叉树2 满二叉树如果一棵二叉树只包含度为0即。

上一篇： 过期域名抢注，过期域名抢注会怎么样

下一篇： 不良图片过滤，不良信息过滤软件