函数连续的条件，函数连续的条件左右都连续且相等吗

连续性的必要条件若函数fx在某点x0无定义，或该点不存在极限，或极限不等于函数值，那么函数在x0处不连续观察图像可以提供直观判断，但这种方法并不严谨记住一些基本初等函数的性质，大多数初等函数在其定义域内都是连续的连续函数的性质包括连续函数的加减乘运算结果仍然连续，复合函数也保持连续性理解函数连续性。

函数连续的条件主要包括以下几点连续性定义若函数$fx$在$x_0$处有定义，且$lim_x to x_0 fx = fx_0$，则称函数$fx$在$x_0$处连续这是函数连续的充要条件，即函数在某点连续的定义充分条件若函数$fx$在$x_0$处可导或可微这些条件比连续更强，则函数在$x_0$处一。

函数fx在x0处连续的三个条件如下1 fx在x0及其左右近旁有定义 解释这意味着函数fx在x=x0这一点以及它附近的点即x0的左侧和右侧都有明确的函数值换句话说，函数在x0处没有“空洞”或“断点”，其定义域包含函数连续的条件了x0及其附近的点2 fx在x0的极限存在 解释极限存在。

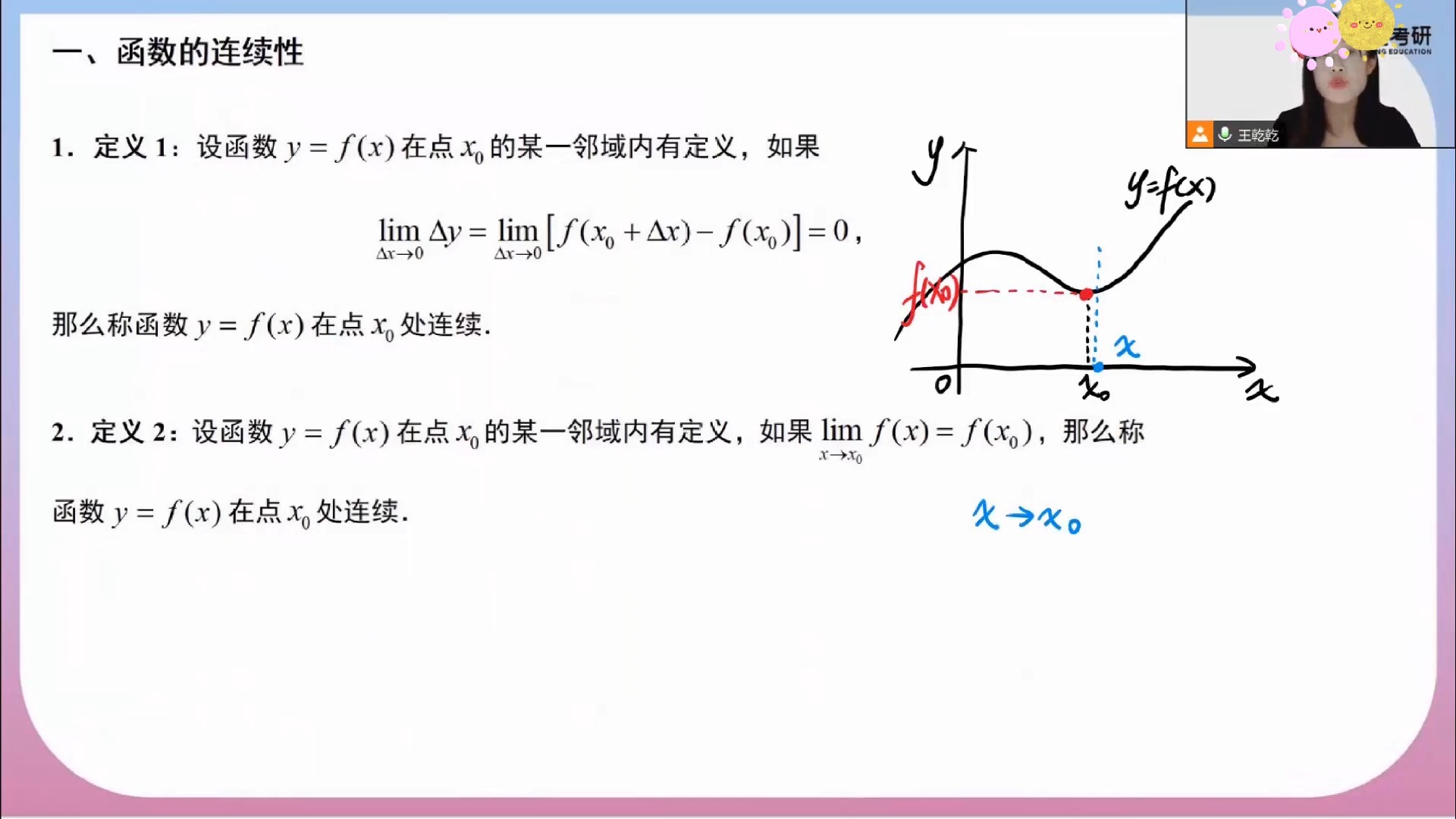
函数连续的条件可以归纳为以下几点1 基本定义条件 若函数$f$在$x0$有定义，且$limx to x_0 f$存在，并且等于$f$，则函数在$x_0$处连续2 充分条件 可导性若函数$f$在$x_0$处可导，则函数在$x_0$处连续 可微性若函数$f$在$x_0$处可微，则函数在$x_0$处。

1除了要求函数在该点连续之外，函数连续的条件我们还需要确保函数在该点的左右两侧都连续换句话说，如果有一个数a小于该点，我们需要找到一个数b大于该点，使得当x从a趋近于该点时，函数值y趋近于L2同时，当x从该点趋近于b时，函数值y也趋近于L如果这两个条件都满足，那么我们就可以说函数在该点。

函数连续的定义基于极限的概念当x趋近于a时，fx的极限等于fa，这是函数连续的充分必要条件函数在某点可导是连续的充分条件，但并非必要条件例如，绝对值函数fx = x在x=0处是连续的，但在此点不可导这是因为绝对值函数在x=0处有一个“尖点”，导致函数在此处无法用单一的导数。

函数f在点x=x0处有定义是f在点x=x0处连续的必要非充分条件要连续，首先必须在这个点有定义但是有定义，还不一定就连续fx在点x=x0处连续，从连续的定义理解是fx点x=x0处左右极限都存在且等于fx0 ，从图像du上看函数曲线在该点是连在一起的在数学中，连续是函数的一种。

上一篇： 凯奇尼古拉斯，凯奇尼古拉斯精灵旅社

下一篇： 刷卡系统，刷卡系统多少钱