01背包问题，01背包问题c语言代码

1 摘要 以背包问题为例01背包问题，介绍01背包问题了贪心法与动态规划01背包问题的关系以及两个方案在解决背包问题上的比较贪心法什么时候能取到最优界并无一般理论01背包问题，但对于普通背包问题我们有一个完美的结果贪心法可取到最优解介绍了其它一些对背包问题的研究或者拓展2 介绍 贪心算法是我们在算法设计技巧与分析这；BIAS0= CMAC，2MAC，2*100BIAS1 = CMAC，12MAC，12*100BIAS2 = CMAC，26MAC，26*100BIAS3 = CMAC，48MAC，48*100HXL=VCAPITAL*100D1=INDEXCD2=MAD1，56DR2=D1D2lt094E1=CHHVC，12HHV；01背包问题的基本思路是每种物品仅有一件，可以选择放或不放使用子问题定义状态，即fiv表示前i件物品恰放入一个容量为v的背包可以获得的最大价值状态转移方程为fiv=maxfi1v，fi1vci+wi，其中fi1v表示不放第i件物品时的最大价值，fi1。

购物单，一个涉及01背包问题的挑战性题目题目要求解决的是如何在有限的购物清单中，挑选出最优组合以满足特定条件看似普通的01背包问题，却因额外的附件约束而增添了几分复杂初次接触此类题目，确实容易让人摸不着头脑通过参考一些题解，我们了解到解决此类问题的关键在于将主件和附件分组考虑考虑；fjwi表示在已经使用容量为jwi时的最大价值fj可以由fjwi这个状态转移到达，表示选取wi这个物品，并从而获得价值为ci而每次fj会在选与不选中决策选出最优的方案从每一个物品，也就是每一个阶段的局部最优推出最后的全局最优值这样就解决了01背包问题；01背包问题描述为给定n件物品，每件物品有确定的重量和价值，以及一个容量为w的背包，要求选择物品使得放入背包的价值总和最大暴力解法使用回溯算法，但效率较低动态规划优化则引入了二维dp数组，其核心在于定义dpij表示从下标为0i的物品里任意取，放进容量为j的背包，价值总和最大是；01背包问题旨在在不超过背包容量的前提下，选择物品组合以实现总价值最大具体来说，给定一个容量为W的背包和n件物品，每件物品都有重量wi和价值vi，目标是寻找一个物品组合，使它们的总重量不超过W，同时总价值达到最大二动态规划方法 适用性动态规划适用于解决那些决策阶段之间相互关联；总之，理解01背包问题的基本思路状态转移的含义以及优化方法，是解决这类问题的关键这个基础模型对其他背包问题的理解和解决具有普适性。

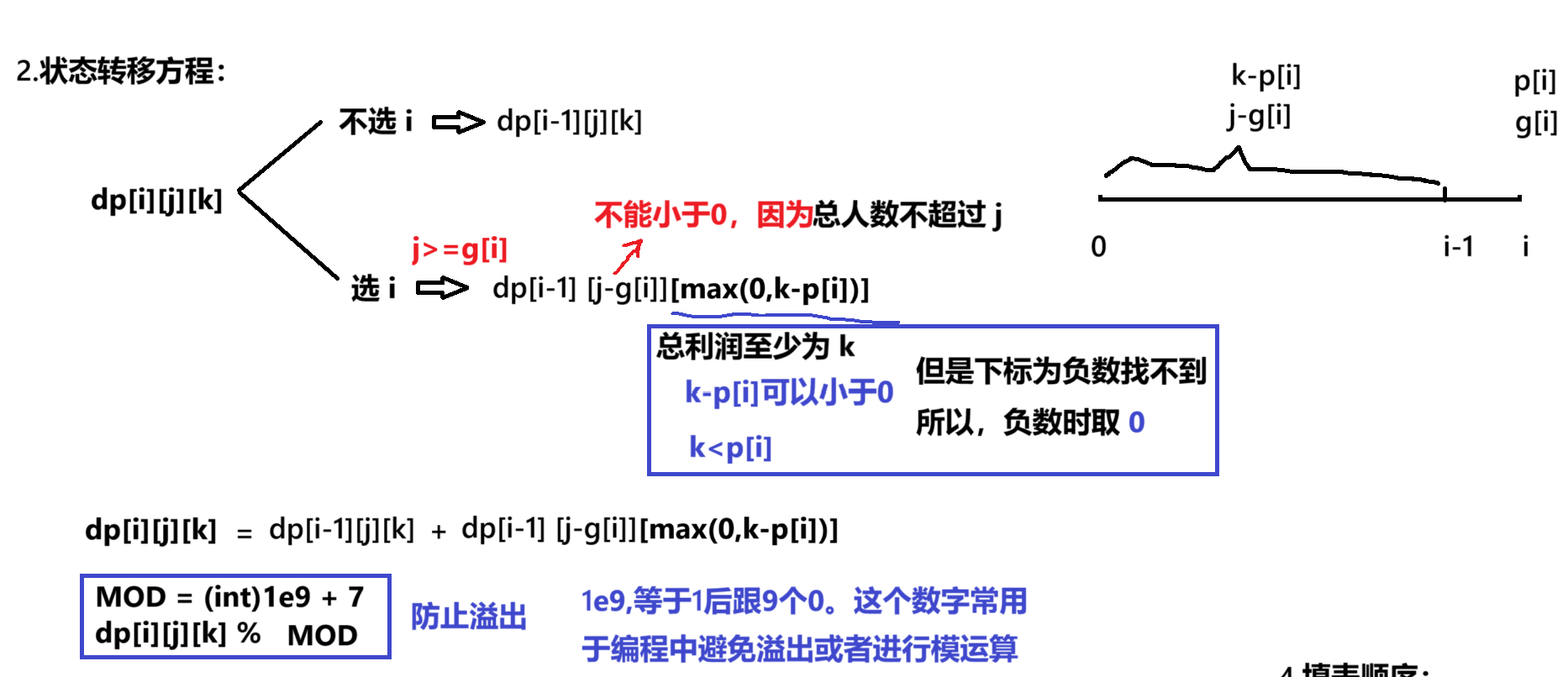
关于背包问题 dp，dp动态规划中的背包问题01这个很多人还不知道，今天来为大家解答以上的问题，现在让我们一起来看看吧11将二维数组转化为一维数组之后，fv表示v的容量最多装多大价值2如果顺序枚举的话，每种物品可能多次使用3例如某个物品重量为5，价值为10，那么就会用f0去更新；01背包问题是最基本的背包问题，它包含了背包问题中设计状态方程的最基本思想，另外，别的类型的背包问题往往也可以转换成01背包问题求解故一定要仔细体会上面基本思路的得出方法，状态转移方程的意义，以及最后怎样优化的空间复杂度P02 完全背包问题 题目 有N种物品和一个容量为V的背包，每种物品都；01背包问题的核心思想是利用动态规划在物品逐一选择与容量逐步增加的考量过程中做出最优决策二状态定义 fiw表示前i个物品装入背包容量为w的最大价值三状态转移方程 fiw = max其中，fi1w表示不装入第i个物品时的最大价值fi1wweighti + valuei表示装入；背包问题和0－1背包问题区别为循环变量不同约束条件不同最大总价值不同一循环变量不同 1背包问题背包问题须先求出列坐标j较小的元素，故让循环变量j的值从小到大递增20－1背包问题0－1背包问题须先求出列坐标j较大的元素，故让循环变量j的值从大到小递减二约束条件不；背包问题中，涉及N种物品和一个容量为V的背包，每种物品无限制目标是找到将哪些物品放入背包，使得总费用不超过背包容量且价值最大化这个问题与01背包问题类似，但区别在于每种物品可以无限取用传统的01背包问题中，策略是取或不取，但在完全背包问题中，策略变为取0件1件2件等状态转移。

01背包问题是什么意思首先，背包问题是一类经典的组合优化问题，即在物品有限的情况下，如何选择一些物品放入背包中，使得这些物品的价值之和最大或者总重量不超过背包容量而01背包问题则是指每个物品只能选择放或者不放，即物品的取舍是二元的其次，01背包问题常用于动态规划的实现在实际应用中；完全背包问题分析1 问题描述有N种物品与容量为V的背包，每种物品数量无限求解在不超重的前提下，总价值最大2 状态表示与01背包一致，为ij，表示在1~i范围内选择物品，体积为j的所有状态集合3 解法1暴力解法，时间复杂度较高解法2状态压缩，一维动态规划，优化目标。

探索算法的奥秘，深入理解背包问题的无限可能九讲背包之旅一一背包问题的基本理念 背包问题，犹如神秘的寻宝游戏，每件物品只能使用一次，目标是找到在背包容量限制下，能带来最大价值的物品组合核心思路是通过物品分类，拆解为子问题，每一次选择都力求价值最大化状态转移方程揭示了这个过程；01背包问题的解答如下1 问题描述01背包问题是一个经典的动态规划问题给定一个背包和N个物品，每个物品有一个重量和一个价值，背包有一个最大承重限制目标是在不超过背包最大承重的前提下，选择一些物品使得它们的总价值最大2 动态规划思路 使用一个二维数组dp，其中dpij表示在。

上一篇： QQ显示IP地址方法开发者社区的简单介绍

下一篇： c语言学习资料，c语言入门经典教材