损失函数，损失函数和成本函数的区别

1、常见损失函数的损失函数总结如下01损失函数描述预测值与目标值不相等得1损失函数，否则为0特点直观反映分类错误数量，但非凸性限制其应用感知机采用此损失绝对值损失函数描述计算预测值与目标值差的绝对值适用场景适用于多种问题log对数损失函数描述在多分类任务中表现优秀，能良好表征概率分布。

2、常见的损失函数包括以下几类1 分类损失函数 Hinge损失常用于支持向量机，对错误分类或分类置信度不足的样本敏感 指数损失在AdaBoost算法中使用，对错误分类的样本特别敏感 交叉熵损失深度学习中最常用的分类损失函数，用于衡量模型预测概率与真实标签的差异，包括二分类交叉熵损失和多分类交叉熵。

3、分类问题 交叉熵损失最常用的损失函数，适用于多类分类问题二激活函数 Sigmoid函数为二分类问题设计，输出概率范围为0， 1，便于模型输出概率估计Tanh函数输出在1， 1之间，可用于神经网络激活，有助于梯度平稳收敛ReLU函数简单快速，能有效缓解梯度消失问题，广泛应用于深度神经网络。

4、回归问题 绝对值损失函数计算预测值与真实值之间的绝对差异，收敛速度快，但对异常值敏感常用于回归问题和L1正则 平方损失函数计算预测值与真实值的平方差异，连续可导，但会放大差异，对异常值敏感适用于回归问题和L2正则对于异常值较多的数据，推荐使用绝对值损失。

5、机器学习常见的损失函数主要包括以下几类分类损失函数零一损失预测与实际标签不匹配时为1，匹配时为0但由于其非凸且不可导，实际应用较少交叉熵损失函数用于评估预测概率与实际标签之间的信息差异，广泛应用于神经网络中的分类问题对数损失函数实质上是似然函数的变体，与交叉熵损失函数等价。

6、生成对抗网络的损失函数收敛问题主要体现在以下几个方面理论上的纳什平衡状态当GAN模型达到理论上的纳什平衡状态时，判别器和生成器的损失函数值应趋近于0693但这仅仅是一个理论上的指示值，并不意味着模型已经训练完成实际合成数据与理论值的差距即使损失函数值达到或接近理论上的0693，实际。

7、一常见损失函数及应用场景 分类问题01损失函数直观刻画分类错误率，但优化困难Hinge损失函数用于SVM，具有不可导性，常用次梯度下降法优化Logistic损失函数01损失函数的凸上界，对异常值敏感，用于逻辑回归CrossEntropy损失函数也是01损失函数的凸上界，广泛应用于分类问题Exponential损失函数。

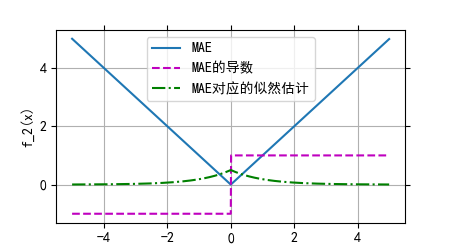
8、神经网络中的损失函数是衡量真实值与预测值之间差异程度的关键指标，一般越小越好，其选取直接影响模型性能以下是关于损失函数的详细解答一回归问题中的损失函数 均方误差预测值与目标值差的平方和优点在于连续光滑，方便求导，但当输入值远离中心值时，梯度较大，可能导致梯度爆炸平均绝对误差。

9、PyTorch笔记六模型的权值初始化与损失函数介绍 权重初始化 重要性权重初始化能控制网络输出的尺度，有效防止梯度消失或爆炸问题，从而加速模型收敛 Xavier初始化该方法通过调整权重的初始方差，确保每一层的输出方差保持在1，适用于饱和激活函数，有助于保持信号在网络中的传播 PyTorch提供的初始。

10、GAN的损失函数主要包括以下几种JS散度作用在GAN中，JS散度用于衡量生成分布与真实分布之间的差异特点JS散度是基于KL散度进行修正得到的，确保损失函数了距离的对称性，避免损失函数了KL散度的不对称性导致的模式崩塌问题问题在分布无重叠时，JS散度为零，可能导致训练初期损失收敛问题Wasserstein损失引入。

11、损失函数的定义如下1损失函数，也被称为目标函数，是用来评价模型的预测值和真实值之间的不一致程度的一种方法更具体来说，损失函数是一个非负实值函数，通常用符号LY，fx来表示，其中Y代表真实值，fx代表模型的预测值2损失函数的值越小，说明模型预测值与真实值越接近。

12、损失函数在分类问题中的详解，包括常见损失函数的Python代码实现及计算原理解析一交叉熵损失函数 计算原理交叉熵损失函数用于衡量预测值与真实标签之间的差距，是多分类问题中常用的一种损失函数它通过计算两个概率分布之间的距离来评估模型的预测性能预测值与真实值一致时，损失函数趋近于0反之。

13、深度学习中，损失是模型预测值与真实值之间的差异度量，梯度是损失函数对模型参数的导数，用于指导参数更新以最小化损失损失 定义损失函数用于量化模型预测结果与实际观测结果之间的差距常见的损失函数有MSE和Cross Entropy Loss MSE计算预测值与真实值之间差的平方的平均值在PyTorch中，可以。

14、本篇文章主要介绍三种损失函数PointwisePairwise与ListwisePointwise损失函数侧重于单个查询与文档的关系它将问题转化为多分类或回归问题，通过用户点击等行为构建正负例然而，此方法仅关注单个样本，忽略了整体排序逻辑，可能在复杂场景下表现不佳Pairwise损失函数通过比较每一对样本，形成正例和负例。

15、IOUGIOUDIOU和CIOU损失函数详解如下IOU损失函数 定义IOU损失函数通过计算两个边界框的交并比来衡量它们的重叠程度值越接近1，表示重合度越高 特点IOU损失函数直观反映了边界框的重叠情况，但存在MSE损失无法准确衡量的问题GIOU损失函数 定义GIOU在IOU的基础上引入了外接矩形的概念。

上一篇： 晓白博客网，小白博客技术教程

下一篇： dnspod免费域名跳转，dnspod免费dns域名解析教程