快速傅立叶变换，离散傅里叶变换和快速傅里叶变换

在计算机世界中快速傅立叶变换，处理连续信号需要借助离散傅里叶变换DFT和快速傅里叶变换FFT尽管真实世界是连续的，但计算机处理的信号是离散的，它无法直接理解和计算积分DFT的目标是理解信号在频域的分布，但计算机对此有限制，只能处理离散的采样值采样是将连续信号转化为离散数据的关键，通过将信号在特定时间；详解快速傅里叶变换FFTFFT是离散傅里叶变换DFT的一种高效算法，它通过迭代方式简化快速傅立叶变换了DFT的乘法运算复杂度原本计算复杂度为公式，FFT将其降低到了公式Cooley和Tukey的标志性论文“An algorithm for the machine calculation of complex Fourier series”虽然在初期遭遇拒稿，但其4页半的简短。

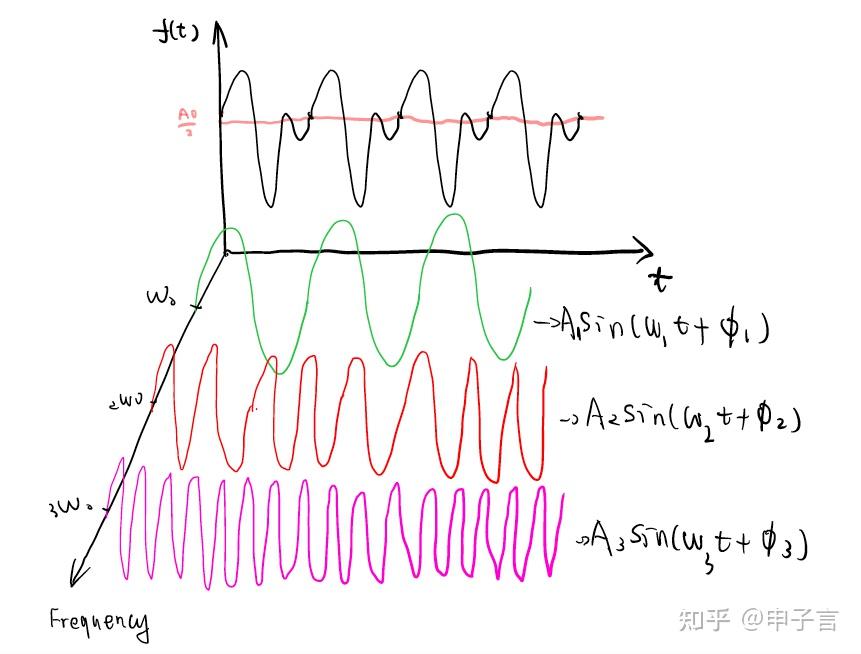
假设两个数互质，那么它们的点离散傅立叶变换点DFT的乘法量可以通过下面的公式计算得出点DFT的乘法量为\N\log_2N\，这里N代表点DFT的大小若我们假设P为一个质数，并且点DFT的乘法量为M，同时在其中，有D1个值不为P的倍数，有D2个值为P的倍数但不为2的倍数，那么N点DFT的乘法量可以；快速傅里叶变换FFT是计算机科学领域中用于高效计算傅里叶变换的方法FFT全称为快速傅氏变换，是离散傅氏变换DFT的一种高效算法这种算法利用了离散傅氏变换中奇偶虚实等特性，对DFT算法进行了优化虽然FFT并没有在傅氏变换的理论方面有新的发现，但在计算机系统或数字系统中应用离散傅。

接着，我们介绍了快速傅里叶变换FFT的概念FFT是DFT的高效算法，通过利用旋转因子的周期性对称性等性质，大幅度减少了计算量当采样点数为2的幂时，FFT的计算速度远超DFT，使得实际应用中能够快速获得信号的频谱信息FFT的物理意义在于揭示信号在频域的特性任何信号都可以被分解为不同频率的。

离散傅里叶变换和快速傅里叶变换

1、快速傅里叶变换Fast Fourier Transform，简称FFT是一种高效的离散傅里叶变换Discrete Fourier Transform，简称DFT的计算方法它是在1965年由JW库利和TW图基提出的FFT通过利用DFT的奇偶虚实特性，对DFT算法进行优化，使得计算机在处理离散傅里叶变换时效率大幅提升FFT的主要特点是计算速度。

2、在快速傅里叶变换FFT的应用中，“补零”是一个常见的操作，本文将从频率分辨率波形分辨率视觉分辨率以及频谱泄漏等方面来阐述其重要性首先，频率分辨率与原始数据的时间长度以及采样频率和参与FFT的数据点数有关当数据点数较少时，频率分辨率较低，难以区分相邻频率的成分此时，可以采用补零的。

3、FFT全称为快速傅立叶变换FFT是“Fast Fourier Transformation”的缩写，即为快速傅氏变换，是离散傅氏变换的快速算法1快速傅里叶变换，即利用计算机计算离散傅里叶变换DFT的高效快速计算方法的统称，简称FT快速傅里叶变换是1965年由JW库利和TW图基提出的采用这种算法能使计算机计算。

4、快速傅里叶变换FFT的核心在于“旋转因子”，它在保持DFT结果不变的同时，处理信号的相位变化上文介绍了蝴蝶操作和“分而治之”策略，现在我们深入理解旋转因子的作用在COMBINE阶段，通过将样本对合并，我们需要计算新的频率分量例如，对于4个点的信号，原DFT测试的是012和3Hz，由于正余弦。

5、快速傅里叶变换是将离散傅里叶变换的过程优化而成的一种算法，通过调整计算顺序和方法，大大降低了计算时间以下是关于FFT的详细解释由来DFT在处理实际采样信号时计算复杂度过高，因此通过优化诞生了FFT原理基础傅里叶变换能够将时域信号转换为频域信号，方便分析信号的频率成分实际应用中，信号均。

6、FTT是快速傅里叶变换的缩写以下是关于FTT的详细解释定义快速傅里叶变换是一种高效的算法，用于计算离散傅里叶变换及其逆变换作用转换信号通过DFT，一个信号可以从时域转换到频域，或者从频域转换到时域降低计算复杂度快速傅里叶变换通过利用DFT的对称性和周期性等性质，显著降低了计算复杂。

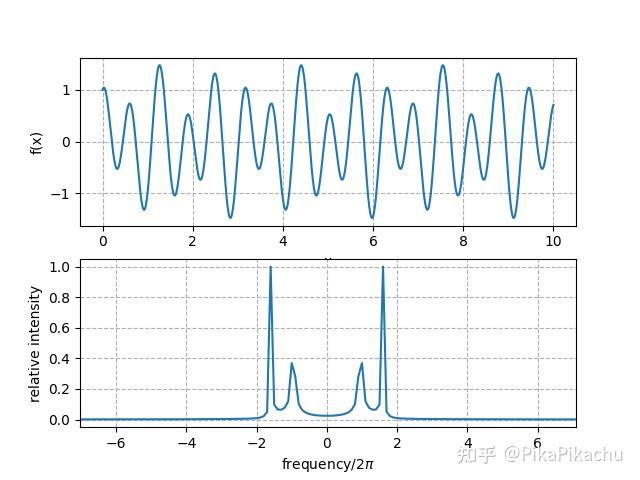
7、快速傅里叶变换FFT是数学算法中的一大瑰宝此算法旨在减少多项式乘法或大整数乘法的复杂度传统的朴素乘法在多项式长度或大整数长度为 n 时，需要进行 n 次乘法运算，效率极低快速傅里叶变换的引入，旨在优化此问题，将其复杂度优化至 On log n多项式的系数表示法是多项式表示的一种，它。

快速傅立叶变换算法

快速傅里叶变换FFT与点数紧密相关，理解这一点需从离散时间傅立叶变换DTFT开始DTFT将离散信号转换至频域，具备周期性，周期为2π其后，离散傅立叶变换DFT等间隔采样DTFT变换后的频域信号周期02π，这里的点数表示对DTFT 02π周期内采样的点数DFT的点数对应于DTFT变换后的频谱。

快速傅里叶变换是离散傅里叶变换的一种高效算法，它通过迭代方式显著降低了DFT的乘法运算复杂度以下是FFT的详解算法背景FFT由Cooley和Tukey提出，其标志性论文虽初期遭遇拒稿，但后来被广泛引用FFT的提出极大地简化了DFT的计算，将原本较高的计算复杂度显著降低核心原理FFT的关键在于复数域内1。

快速傅里叶变换 fast Fourier transform， 即利用计算机计算离散傅里叶变换DFT的高效快速计算方法的统称，简称FFT快速傅里叶变换是1965年由JW库利和TW图基提出的采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就。

将这种策略应用到快速傅里叶变换中，我们首先将大问题分解具体而言，我们首先将问题分为两步划分和合并划分阶段包括将原始信号分解为较小的组，而合并阶段则涉及计算各组的傅里叶变换在傅里叶变换中，我们关注周期性信号对于一个周期为T的余弦波或正弦波，每隔一个周期的点对，它们的复指数是。

上一篇： sqlsparksql:查询中的if语句语法的简单介绍

下一篇： 魔兽世界宏命令教程，魔兽世界宏命令教程 使用两个技能