关于傅里叶变换的意义和理解(通俗易懂)的信息

一意义从现代数学的眼光来看傅里叶变换的意义和理解(通俗易懂)，傅里叶变换是一种特殊的积分变换它能将满足一定条件的某个函数表示成正弦基函数的线性组合或者积分在不同的研究领域，傅里叶变换具有多种不同的变体形式，如连续傅里叶变换和离散傅里叶变换在数学领域，尽管最初傅里叶分析是作为热过程的解析分析的工具，但是其。

通过这样的描述，傅里叶变换的意义和理解(通俗易懂)我们可以更加具体地理解离散时域信号的傅里叶变换这种周期性的频域表示，不仅揭示傅里叶变换的意义和理解(通俗易懂)了信号在时域中的频率成分，也展示了信号在频域中的周期性重复特性，这对于信号分析和处理具有重要意义深入理解傅里叶变换的性质，可以帮助傅里叶变换的意义和理解(通俗易懂)我们更好地掌握数字信号处理的基础知识，为后续的信号分析和处理打。

傅里叶变换的物理意义是把非周期信号用无限的周期正余弦函数进行叠加，以表示所需的时域函数进行傅里叶变换的原因主要有以下几点揭示频域特性时域内难以观察的特性很多在时域内难以直接观察或分析的特性，在频域内却能清晰地展现例如，矩形波在时域内看起来只是一条直线，但通过傅里叶变换，我们。

傅里叶变换的物理意义是把非周期信号用无限的周期正余弦函数进行叠加，来表示所需要的时域函数进行傅里叶变换的原因主要有以下几点揭示时域内难以观察的特性很多在时域内难以观察或分析的特性，在频域内却能清晰地展现例如，矩形波在时域内看似简单的直线，但通过傅里叶变换后，在频域内可以观察到。

更为直观地说，傅里叶变换就像是一个信号的“解码器”，它能够揭示隐藏在复杂时序数据中的频率模式无论是声音中的不同音调，还是图像中的色彩和纹理，都可以通过傅里叶变换分解为基本的频率成分，使我们能够更好地理解和处理这些信号总的来说，理解傅里叶变换就是掌握了一个解锁复杂信号世界的关键。

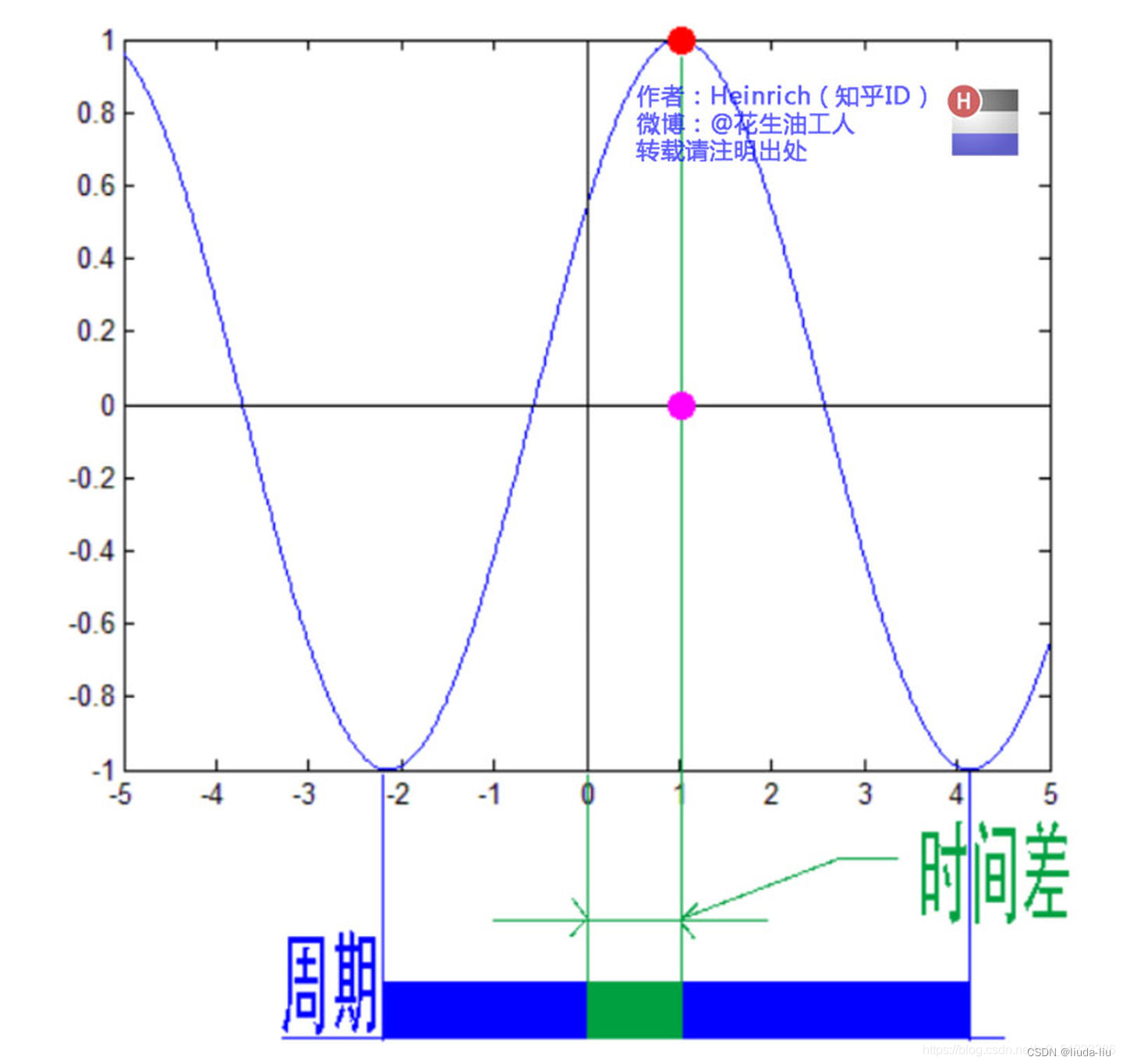
意义傅里叶变换的实质是将一个信号分离为无穷多多正弦复指数信号的加成，也就是说，把信号变成正弦信号相加的形式既然是无穷多个信号相加，那对于非周期信号来说，每个信号的加权应该都是零但有密度上的差别，你可以对比概率论中的概率密度来思考一下落到每一个点的概率都是无限小，但。

1傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数正弦和或余弦函数或者它们的积分的线性组合在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换最初傅立叶分析是作为热过程的解析分析的工具被提出的2傅里叶级数和傅里叶变换其实就是。

傅里叶变换的物理意义，无需多讲，就是把非周期信号，用无限的周期正余弦函数进行叠加，来表示所需要的时域的函数做傅里叶变换的目的是因为 很多在时域内看不见的特性在频域内能很清楚的得到比如说，矩形波，在时域内就一直线，当用傅里叶变换后在频域内，我们就能看见像各谐波的频率，相位，振幅。

傅里叶变换的意义一傅里叶变换是一种数学工具，它将信号从时间域转换到频率域它在科学和工程领域中有着广泛的应用，尤其在信号处理图像分析通信等领域通过傅里叶变换，我们可以更深入地理解和分析信号的特性二信号分解 傅里叶变换能够将复杂的信号分解成不同频率的简单信号，这些信号。

对于一个简单的正弦波信号，经过采样和FFT处理，可以在频域上观察到一个清晰的频率尖峰对于实际的音频信号，如语音剪辑，通过FFT分析可以观察到多个频率成分的存在，这些频率成分共同构成了语音信号的特征意义与价值傅里叶变换为我们提供了一种理解和分析复杂信号的有效方法在音频处理图像处理信号。

进而计算出系统的能量谱线型，如洛伦兹线型傅立叶变换的实质在于通过分解或换基，揭示信号或函数的内在结构这种变换的物理意义和应用广泛，从信号处理到图像分析，再到量子力学，都离不开傅立叶变换的理论与实践掌握变换的原理，理解其在不同场景下的应用，是深入学习和应用该技术的关键。

傅里叶变换把信号由时域转为频域，因此把不同频率的信号在时域上拼接起来进行傅里叶变换是没有意义的实际情况下，我们隔一段时间采集一次信号进行变换，才能体现出信号在频域上随时间的变化我的语言可能比较晦涩，但我已尽我所能向你讲述我的一点理解真心希望能对你有用我已经很久没在知道。

要知道傅立叶变换算法的意义，首先要了解傅立叶原理的意义傅立叶原理表明任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率振幅和相位和傅立叶变换算法对应的是反傅。

和傅立叶变换算法对应的是反傅立叶变换算法该反变换从本质上说也是一种累加处理，这样就可以将单独改变的正弦波信号转换成一个信号傅里叶变换的作用 傅里叶变换的作用就是把非正余弦周期请注意必须是周期函数函数转化为无限个规则的正弦余弦函数变成规则的函数以后，虽然有无限项，但是工程取前。

F = intfe^ dt 其中，F 是信号的频域表示，f 是信号的时域表示，omega 是角频率，j 是虚数单位这个公式表示了时域到频域的转换而其逆变换，即从频域到时域的公式为f = int Fe^ domega这个公式表示了频域信号如何被还原为时域信号3 傅里叶变换的意义 傅里叶变换的重要性。

下面从公式解释下傅里叶变换的意义因为傅里叶变换的本质是内积，所以ft和求内积的时候，只有ft中频率为的分量才会有内积的结果，其余分量的内积为0可以理解为ft在上的投影，积分值是时间从负无穷到正无穷的积分，就是把信号每个时间在的分量叠加起来，可以理解为ft在上的投影的叠加。

周期离散时间傅里叶变换对于周期离散时间信号，通过特定的公式将其映射到频域，实现信号的坐标转换非周期信号的傅里叶变换对于非周期信号，通过补值技巧将其与周期信号的傅里叶变换公式建立起联系，当信号的周期无限大时，通过积分将其转换为连续信号的处理方式傅里叶变换的深刻意义简化分析傅。

上一篇： iframe属性，iframe的window属性

下一篇： R语言可视化mdashmdashggplot图表中的线条的简单介绍