fft算法，fft算法详解

1、2 算法实现优化在FFT算法中fft算法，反转操作有助于更高效地进行计算它使得算法可以利用分治策略，将大fft算法的DFT分解为多个较小fft算法的DFT比如通过将序列按特定规则反转后进行分组计算，能大大减少计算量，提高计算速度3 对称性体现反转后的序列能更好地体现出信号的对称性等特性这对于分析信号的各种特征很；首先，FFT算法通过相位因子解决所有点对的蝴蝶操作，将2个样本组合为4个样本点，进而构建出四组4点蝴蝶，再将它们组合成两组8点蝴蝶，最终形成一组16点蝴蝶结果呈现为16个不同频率的正弦波列表在FFT过程中，每个4点蝶形包含两个旋转因子，每个8点蝶形则包含四个旋转因子，旋转因子数量为蝶形中点；2 频率抽取FFT 原理从频域信号序列入手，将其分为奇偶两部分，通过逐级运算，将N点的计算分解为N2次，减少乘法次数 过程以N=2为例，将输入序列分为前后两半，通过两次加减法和一次乘法，得到两个子序列的频域信息基2的FFT基本蝶形运算遵循类似的计算流程3 其他FFT算法 除fft算法了基2的；旋转因子通过复数乘法的方式来实现信号的平移在FFT算法中，复数乘法不仅改变了信号的幅度，还改变了信号的相位因此，通过选择合适的旋转因子，我们可以实现信号的平移操作以i为例，它相当于将信号向右平移了90度这个平移操作可以通过乘以i来实现，也可以通过按三角函数平移π2来实现，两者的结果；基2FFT算法的过程主要包括以下步骤输入信号将要进行傅里叶变换的离散信号表示为长度为N的复数序列x^0^，x^1^x^N1^这是FFT算法的起始输入奇偶分离将输入序列按照索引的奇偶性分为两个子序列奇数索引序列为x^1^，x^3^x^N1^，偶数索引序列为。

2、数据访问顺序匹配FFT算法采用分治策略，将输入序列递归分解为更小的子问题位反转通过将数据索引的二进制表示前后颠倒如索引3的二进制011变为110，即6，使数据在内存中的排列顺序与算法自然分解后的访问顺序完全一致这种匹配避免了分治过程中因顺序错位导致的额外计算开销，确保蝶形运算能直接按预期顺；FFT算法通过分治策略如基2FFT将长序列分解为短序列，递归处理后再合并结果这一过程中，蝶形运算的本质是对周期延拓后的子序列进行相位校正和叠加例如，在8点FFT中，输入序列被视为周期为8的无限序列，分解后的4点子序列同样具有周期性周期延拓特性使得FFT能够高效利用子序列的对称性，将计算。

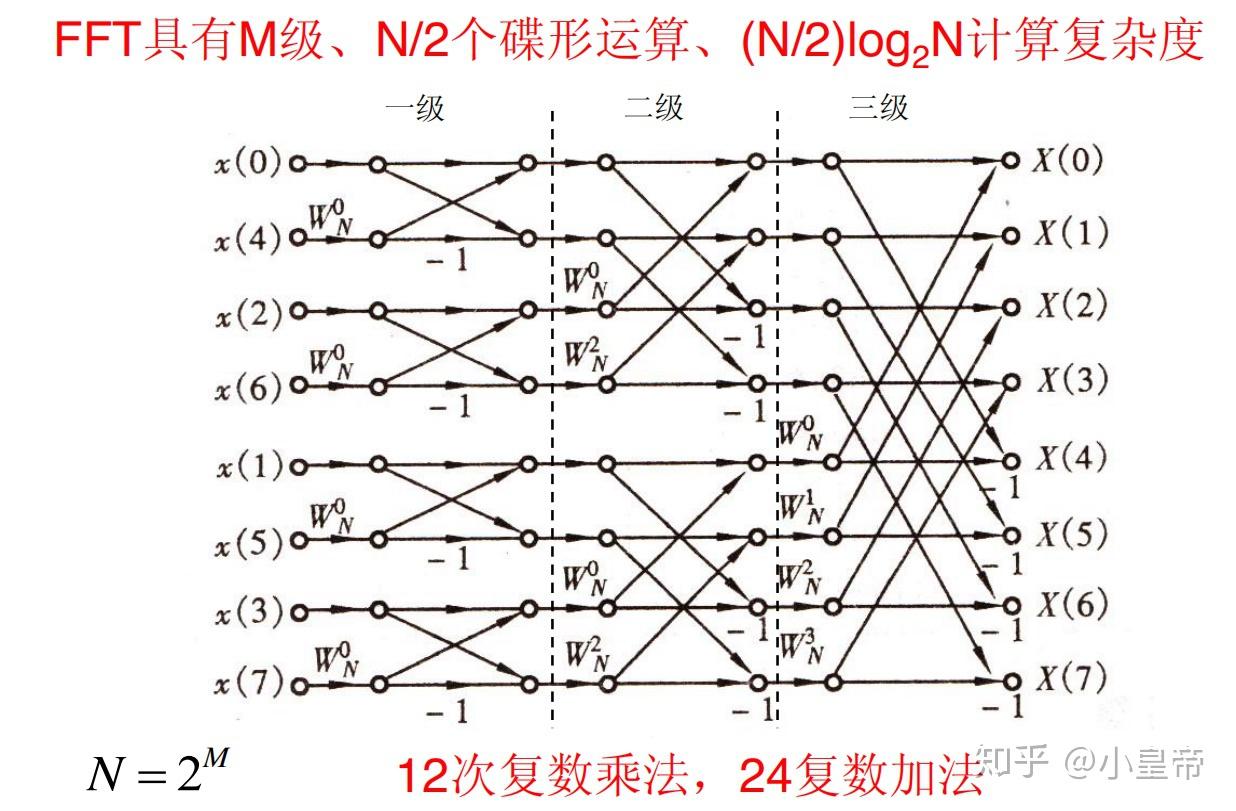
3、FFT通过递归地将计算任务分解，利用公式和公式的周期性，以及公式的对称性输入序列在FFT中的计算结果按二进制反转排序，进一步简化了计算过程矩阵分解视角从矩阵分解角度看，FFT可以将稠密矩阵分解为三个特殊稀疏矩阵的乘积这种分解展示了FFT算法的直观结构，使得计算更加高效推荐学习资源；FFT的计算原理主要是利用DFT中的周期性和对称性，将整个DFT的计算变成一系列迭代运算，从而大幅度提高运算效率FFT算法的主要分类包括按时间抽取算法如基2算法也称为库利图基算法DITFFT按频率抽取算法如基2算法也称为桑德图基算法DIFFFT进行FFT计算时的注意事项要求输入；在FFT算法中，通常会将输入信号分成长度为2的幂次方的序列，然后利用蝶形运算Butterfly Operation进行迭代计算蝶形运算的本质是利用DFT的对称性和周期性，将长序列的DFT分解为短序列的DFT之和或差四总结 快速傅里叶变换FFT是计算离散傅里叶变换DFT及其逆变换的高效算法虽然FFT本身不；FFT算法是一种高效的快速傅立叶变换方法，它通过将长序列的离散傅立叶变换DFT逐步分解为较短序列的DFT来实现这一过程不仅简化了计算，还大大提高了运算速度根据抽取方式的不同，FFT算法可以分为DITFFT按时间抽取和DIFFFT按频率抽取两大类DITFFT的特点是将输入序列按照时间顺序分组。

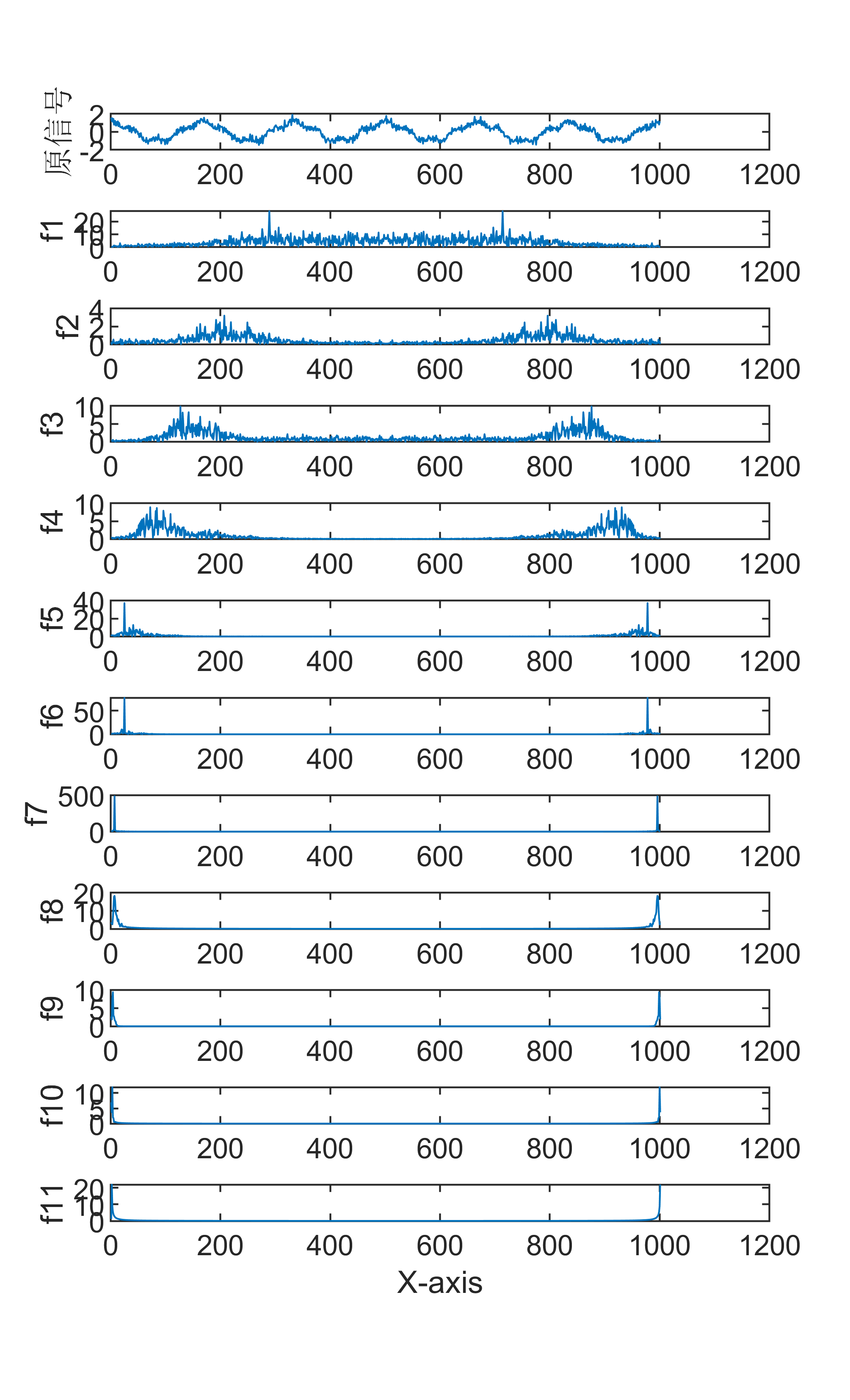
4、FFT算法将原始信号分解为多个频率的正弦波分量表格中的每个复数都对应一个特定的频率分量，这些频率分量在频域上均匀分布幅度和相位复数的模表示了该频率分量在信号中的强度或大小复数的辐角表示了该频率分量相对于参考点的相位偏移频谱图和相位图通过FFT算法输出的复数表格，可以绘制出频谱图和相位图频谱图展示了信号在；FFT算法的基本原理是利用离散傅里叶变换的对称性周期性和稀疏性，通过数学变换和重排，将原始的N点DFT分解为多个较小的DFT，从而大大减少计算量，提高计算效率具体来说，FFT算法的基本原理包括以下几点分解思想FFT算法将原始的N点DFT分解为两个N2点的DFT这两个N2点的DFT再继续分解，直到；FFT算法的基本原理如下1将输入序列分成偶数和奇数下标两个子序列2对这两个子序列分别进行递归调用FFT算法，得到它们的DFT结果3根据傅里叶变换的性质，可以通过这两个子序列的DFT结果计算出原始序列的DFT结果重复上述步骤，直到最后得到的序列长度为1，即得到了原始序列的DFT结果FFT算法的概念FFT快速傅里叶变；在排序之后，接下来是加权过程在FFT8中，相乘的两个位置为奇数位的需要乘一个旋转因子Wn0旋转因子是FFT算法中的一个关键元素，它决定了不同频率分量的相位和幅度通过乘以旋转因子，可以实现对输入数据的加权处理，从而为后续的蝶形算法过程做好准备3 蝶形算法过程 蝶形算法是FFT算法；CooleyTukey FFT算法的核心要点如下张量积表示CooleyTukey FFT算法可以通过张量积的形式进行描述，这种表示方法直观且简洁在算法中，内部操作可以被表示为两个较小规模FFT操作的张量积，这有助于揭示算法的内在结构矩阵分解与表示8点FFT的矩阵表示可以通过矩阵分解进行重写，以便于理解分解后的矩阵。

上一篇： 反ps技术，反ps工具软件下载

下一篇： 怎样提高电脑速度，怎么有效提升电脑速度